

Разработчики проводят недели, анализируя сотни вопросов для интервью на сайтах вроде LeetCode, — пишет tproger.ru в своем переводе статьи «14 Patterns to Ace Any Coding Interview Question». Одна из наиболее распространённых причин беспокойства перед интервью: достаточно ли я прорешал практических заданий? Мог ли я сделать больше?
Вот почему я стараюсь помочь разработчикам понять шаблоны, лежащие в основе каждого вопроса. Если вы поймёте эти 14 шаблонов, то сможете использовать их для решения множества задач. Я расскажу, как определить подходящий шаблон, и дам несколько примеров для каждого. Но это всё довольно поверхностно — я настоятельно рекомендую изучить Grokking the Coding Interview: Patterns for Coding Questions для пояснений, примеров и практики.
Предполагается, что вы разбираетесь в структурах данных. Если нет, ознакомьтесь с этими курсами повышения квалификации по структурам данных или загляните в наш раздел по алгоритмам и структурам данных.
14 шаблонов, которые мы рассмотрим сегодня:
- Скользящее окно.
- Два Указателя или Итератора.
- Быстрые и медленные Указатели или Итераторы.
- Слияние интервалов.
- Циклическая сортировка.
- Разворот связанного списка.
- Дерево BFS.
- Дерево DFS.
- Две кучи.
- Подмножества.
- Модифицированный бинарный поиск.
- Топ К-элементов.
- K-way слияние.
- Топологическая сортировка.
1. Скользящее окно
Шаблон скользящего окна используется для выполнения операции с определённым размером окна данного массива или связанного списка, например для поиска самого длинного подмассива, содержащего все 1. Скользящие окна начинаются с 1-го элемента, продолжают смещаться вправо на один элемент и регулируют длину окна в соответствии с задачей, которую вы решаете. В некоторых случаях размер окна остаётся постоянным, а в других — увеличивается или уменьшается.
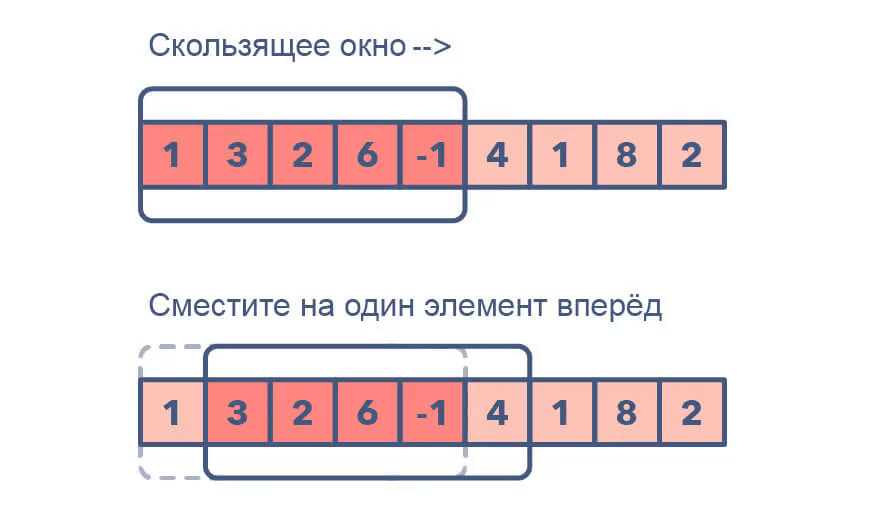

Как определить, когда использовать шаблон скользящего окна:
- входные данные задачи — это линейная структура данных, например связанный список, массив или строка;
- нужно найти самую длинную/короткую подстроку, подмассив или желаемое значение.
Задачи, для которых подойдёт шаблон скользящего окна:
- максимальная сумма подмассива размера «K» (лёгкий);
- самая длинная подстрока с различными «K» символами (средний);
- анаграммы строки (сложный).
2. Два Указателя или Итератора
Это шаблон, в котором два указателя перебирают структуру данных в тандеме, пока один или оба указателя не достигнут определённого условия. Два указателя часто полезны при поиске пар в отсортированном массиве или связанном списке. Например, когда нужно сравнить каждый элемент массива с другими его элементами.
С одним указателем пришлось бы постоянно возвращаться назад через массив, чтобы найти ответ. Так же, как и с одним итератором, это неэффективно для временной и пространственной сложности — концепции, называемой асимптотическим анализом. Хотя решение в лоб с одним указателем будет работать, его сложность — около O (n²). Во многих случаях два указателя помогут найти решение с лучшей временной и пространственной сложностью.
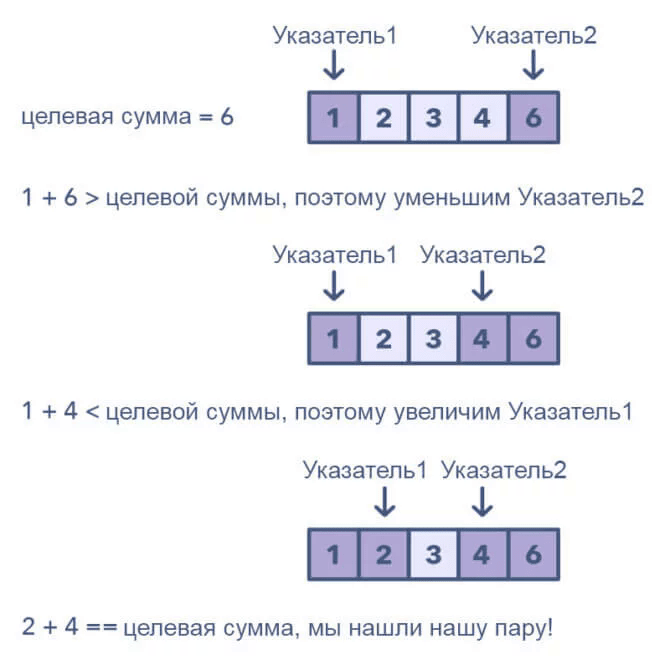

Как определить, что подойдёт шаблон двух указателей:
- вы имеете дело с отсортированными массивами (или связанными списками), и вам необходимо найти набор элементов, которые удовлетворяют определённым ограничениям;
- набор элементов в массиве представляет собой пару, триплет или даже подмассив.
Задачи, для которых подойдёт шаблон двух указателей:
- возведение в квадрат отсортированного массива (лёгкий);
- триплеты, суммирующие до нуля (средний);
- сравнение строк, содержащих пробелы (средний).
3. Быстрые и медленные указатели
Подход быстрого и медленного указателя, также известный как алгоритм зайца и черепахи, использует два указателя, которые перемещаются по массиву (или последовательности / связному списку) с разными скоростями. Этот подход полезен при работе с циклически связанными списками или массивами.
Двигаясь с разными скоростями (скажем, в циклически связанном списке), алгоритм доказывает, что эти два указателя обязательно встретятся. Быстрый указатель должен перехватывать медленный, когда оба указателя находятся в цикле.
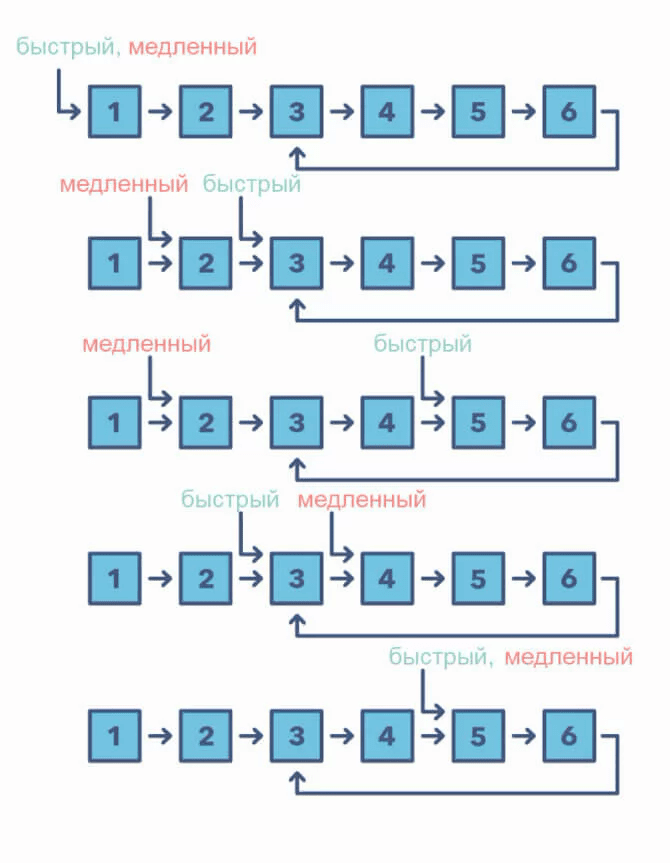

Как определить, когда использовать шаблон быстрого и медленного указателя:
- задача касается цикла в связанном списке или массиве;
- нужно узнать положение определённого элемента или общую длину связанного списка.
Когда использовать его вместо двух указателей?
- В некоторых случаях не следует использовать шаблон Двух указателей, например в одном списке, где вы не можете двигаться в обратном направлении. Использовать этот шаблон нужно, когда вы пытаетесь определить, является ли связанный список палиндромом.
Задачи, для которых подойдёт шаблон быстрого и медленного указателей:
- цикл связанного списка (лёгкий);
- является ли связанный список палиндромом (средний);
- цикл в круговом массиве (сложный).
4. Слияние интервалов
Эффективный метод работы с пересекающимися интервалами. В большинстве задач, связанных с интервалами, нужно либо найти пересекающиеся интервалы, либо совместить интервалы, если они пересекаются. Шаблон работает так:
Для двух интервалов («a» и «b»), есть два способа, которыми эти интервалы могут быть связаны друг с другом:
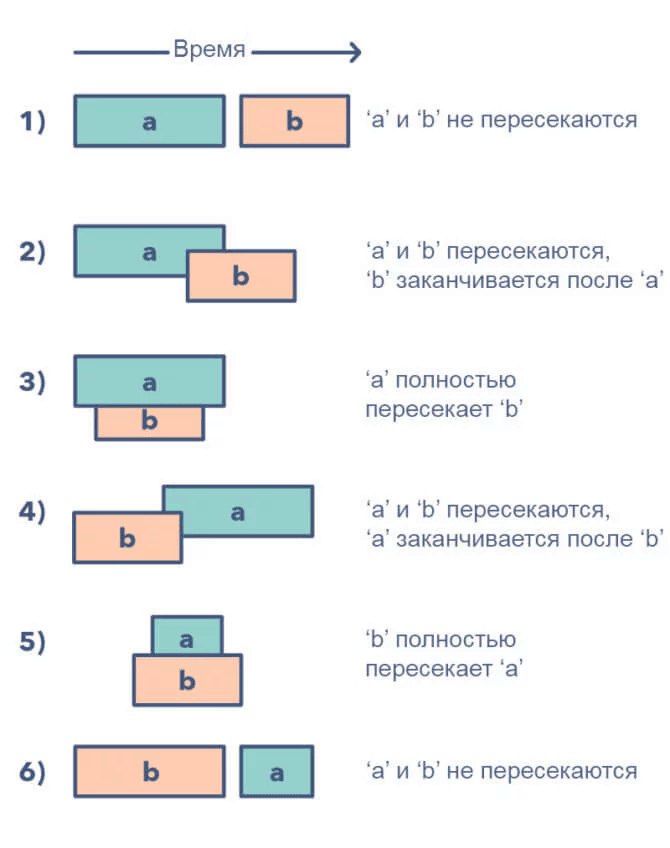

Понимание этих шести случаев позволит решить широкий спектр задач — от вставки интервалов до оптимизации слияний интервалов.
Как определить, что подойдёт шаблон слияния интервалов?
- нужно составить список только с взаимоисключающими интервалами;
- вы слышите термин «пересекающиеся интервалы».
Задачи, для которых подойдёт шаблон слияния интервалов:
- пересечение интервалов (средний);
- максимальная нагрузка на процессор (сложный).
5. Циклическая сортировка
Интересный подход для решения задач, которые связаны с массивами, содержащими числа в заданном диапазоне. Шаблон циклической сортировки выполняет итерацию по массиву по одному числу за раз, и если текущее число, которое вы перебираете, не соответствует правильному индексу, вы меняете его местами с числом по правильному индексу. Можете попытаться поместить число, с которым мы поменяли текущее число, в правильный индекс, но это приведет к сложности O (n²), поэтому больше подойдёт метод циклической сортировки.


Как определить, когда использовать шаблон циклической сортировки:
- в задачах с использованием отсортированного массива с числами в заданном диапазоне;
- если нужно найти отсутствующее/дублированное/наименьшее число в отсортированном/повёрнутом массиве.
Задачи, для которых подойдёт шаблон циклической сортировки:
- найти недостающий номер (лёгкий);
- найти наименьшее недостающее положительное число (средний).
6. Разворот связанного списка
Вас могут попросить инвертировать связи между набором узлов связанного списка. Часто это нужно сделать на месте, то есть используя существующие объекты узла и не используя дополнительную память.
Шаблон меняет местами только один узел, начиная с одной переменной (current), указывающей на головной элемент связанного списка, а другая переменная (previous) будет указывать на предыдущий узел, который вы обработали. Шаг за шагом вы развернёте узел, наведя его на предыдущий, прежде чем перейти к следующему узлу. Кроме того, вы обновите переменную previous, чтобы всегда указывать на предыдущий узел, который вы обработали.
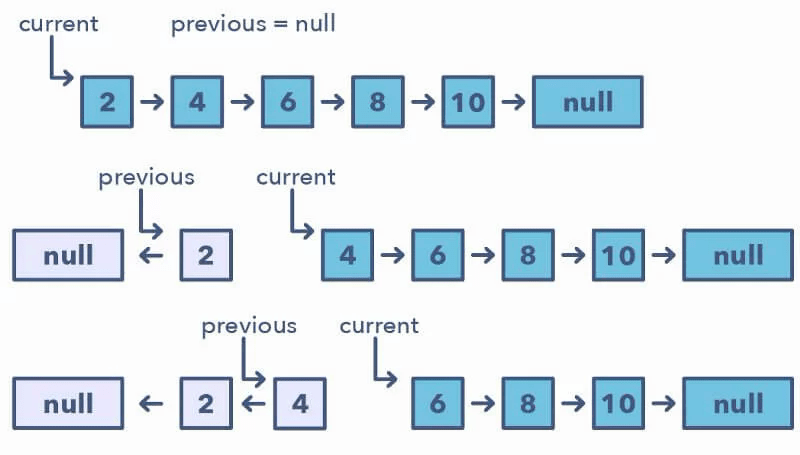

Как определить, когда использовать шаблон разворот связанного списка:
- если вас попросили развернуть связанный список без использования дополнительной памяти.
Задачи, для которых подойдёт шаблон разворот связанного списка:
- перевернуть подсписок (средний);
- перевернуть каждый K-элемент подсписка (средний).
7. Дерево BFS
Этот шаблон основан на методе поиска в ширину (BFS) для обхода дерева и использует очередь для отслеживания всех узлов уровня перед переходом на следующий уровень. Любая задача, связанная с обходом дерева в поэтапном порядке, может быть эффективно решена с помощью этого подхода.
Дерево BFS работает, помещая корневой узел в очередь, а затем непрерывно повторяясь, пока очередь не станет пустой. Для каждой итерации мы удаляем узел в начале очереди и «посещаем» этот узел. После удаления каждого узла из очереди мы также вставляем все его дочерние элементы в очередь.
Как определить, когда использовать шаблон дерево BFS:
- вас просят обойти дерево поэтапно (или поуровнево).
Задачи, для которых подойдёт шаблон дерево BFS:
- поуровневый обход двоичного дерева (лёгкий);
- зигзагообразный обход (средний).
8. Дерево DFS
Дерево DFS основано на методе поиска в глубину (DFS) для обхода дерева.
Можете использовать рекурсию (или стек для итеративного подхода), чтобы отслеживать все предыдущие (родительские) узлы при обходе.
Дерево DFS работает начиная с корня дерева. Если узел не является листом, нужно сделать две вещи:
- Решить, обрабатывать ли текущий узел сейчас (прямой обход), между обработкой двух дочерних элементов (центрированный обход) или после обработки обоих дочерних элементов (обратный обход).
- Сделать два рекурсивных вызова для обоих потомков текущего узла, чтобы обработать их.
Как определить, когда использовать шаблон дерево DFS:
- вас просят совершить прямой, центрированный или обратный обход дерева;
- требуется найти что-то, где узел ближе к листу.
Задачи, для которых подойдёт шаблон дерево BFS:
- сумма номеров путей (средний);
- все пути для суммы (средний).
9. Две кучи
Во многих задачах дан набор элементов, которые можно разделить на две части. Чтобы решить задачу, нужно знать наименьший элемент в одной части и наибольший в другой.
Этот шаблон использует две кучи: Min Heap, чтобы найти самый маленький элемент, и Max Heap, чтобы найти самый большой. Шаблон работает, сохраняя первую половину чисел в Max Heap, потому что вы ищите наибольшее число в первой половине. Затем вы сохраняете вторую половину чисел в Min Heap, так как хотите найти наименьшее число во второй половине. В любой момент медиана текущего списка чисел может быть вычислена из верхнего элемента двух куч.
Как определить, когда использовать шаблон две кучи:
- приоритетные очереди, планирование;
- нужно найти самые маленькие / самые большие / медианные элементы набора;
- иногда полезен в задачах с бинарной структурой данных.
Задачи, для которых подойдёт шаблон две кучи:
- найти медиану потока чисел (средний).
10. Подмножества
Огромное количество задач на собеседовании связано с перестановками и комбинациями заданного набора элементов. Шаблон подмножества описывает эффективный метод поиска в ширину (BFS) для их решения.
Шаблон выглядит так:
Дан набор из [1, 5, 3].
- Начните с пустого набора: [[]].
- Добавьте первое число (1) ко всем существующим подмножествам, чтобы создать новые подмножества: [[], [1]].
- Добавьте второе число (5) ко всем существующим подмножествам: [[], [1], [5], [1,5]].
- Добавьте третье число (3) ко всем существующим подмножествам: [[], [1], [5], [1,5], [3], [1,3], [5,3], [1, 5,3]].
Наглядное представление шаблона подмножества:
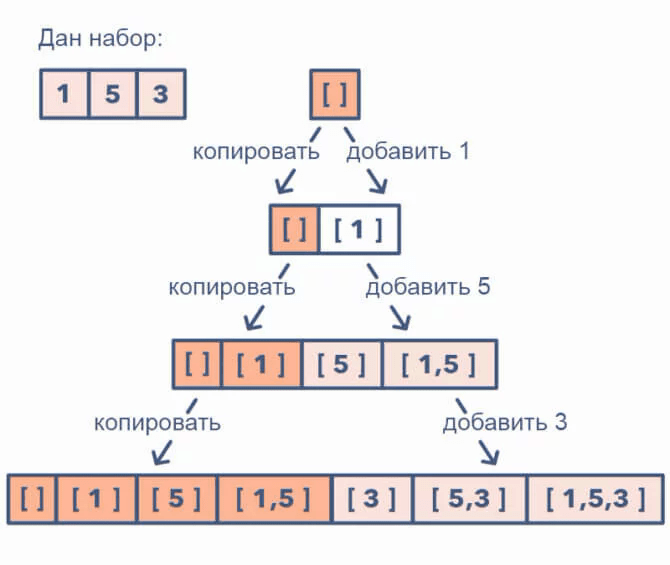

Как определить, когда использовать шаблон подмножества:
- нужно найти комбинации или перестановки заданного набора.
Задачи, для которых подойдёт шаблон подмножества:
- подмножества с дубликатами (лёгкий);
- перестановки строк при изменении регистра (средний).
11. Модифицированный бинарный поиск
Когда вам дают отсортированный массив, связанный список или матрицу и просят найти определённый элемент, лучшим алгоритмом будет бинарный поиск. Этот шаблон описывает эффективный способ решения всех задач, связанных с бинарным поиском.
Для набора по возрастанию шаблоны выглядят так:
- Сначала найдите середину начала и конца. Простой способ найти середину был бы: middle = (start + end) / 2. Но от этого может быть целочисленное переполнение, поэтому рекомендуется представлять середину как: middle = start + (end – start) / 2.
- Если ключ равен числу в середине индекса, верните середину.
- Если «ключ» не равен середине индекса:
- Если ключ < arr [middle], уменьшите поиск до end = middle — 1.
- Если ключ > arr [middle], уменьшите поиск до to end = middle + 1.
Наглядное представление шаблона модифицированный бинарный поиск:
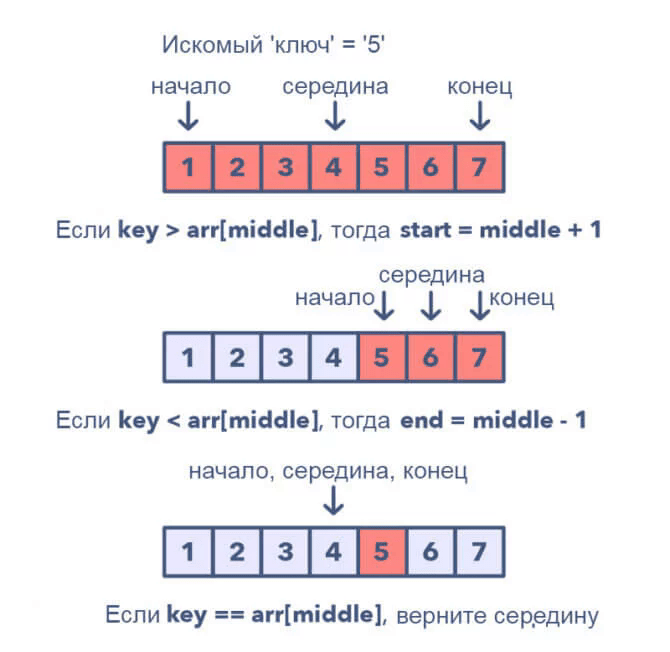

Задачи, для которых подойдёт шаблон модифицированный бинарный поиск:
- Бинарный поиск, не зависящий от порядка (лёгкий);
- Поиск в отсортированном бесконечном массиве (средний).
12. Топ К-элементов
Любая задача, в которой требуется найти самые большие / самые маленькие / частые K-элементы среди данного набора, подпадает под этот шаблон.
Лучшая структура данных для отслеживания K-элементов — куча. Этот шаблон будет использовать кучу для решения задач, связанных с K-элементами одновременно из набора заданных элементов. Шаблон выглядит так:
- Вставьте K-элементы в Min-heap или Max-heap в зависимости от задачи.
- Выполните итерации по оставшимся числам и, если найдёте число, которое больше, чем у вас в куче, удалите это число и вставьте большее.


Нет необходимости в алгоритме сортировки, потому что куча будет отслеживать элементы для вас.
Как определить, когда использовать шаблон Топ К-элементов:
- если нужно найти самые большие / самые маленькие / частые K-элементы в данном наборе;
- если нужно отсортировать массив, чтобы найти верный элемент.
Задачи, для которых подойдёт шаблон Топ К-элементов:
- топ K-номеров (лёгкий);
- топ K-частых номеров (средний).
13. K-Way слияние
K-way слияние поможет решить задачи, связанные с набором отсортированных массивов.
Когда вам дают отсортированные K-массивы, вы можете использовать кучу для эффективного выполнения отсортированного обхода всех элементов всех массивов. Можете поместить наименьший элемент каждого массива в Min Heap, чтобы получить общий минимум. После этого поместите следующий элемент из того же массива в кучу. Затем повторите, чтобы сделать отсортированный обход всех элементов.
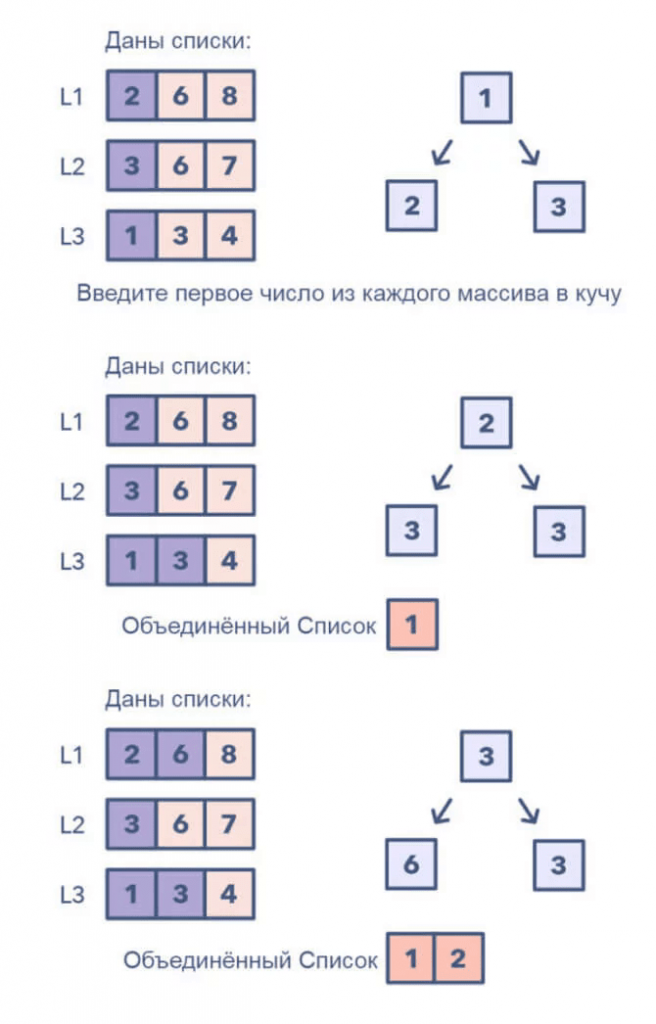

Шаблон выглядит так:
- Вставьте первый элемент каждого массива в Min Heap.
- Извлеките самый маленький (большой) элемент из кучи и добавьте в объединённый список.
- После удаления наименьшего элемента из кучи вставьте следующий элемент из того же списка в кучу.
- Повторите шаги 2 и 3, чтобы заполнить объединённый список в отсортированном порядке.
Как определить, когда использовать шаблон K-Way слияние:
- задача состоит из отсортированных массивов, списков или матрицы;
- требуется объединить отсортированные списки или найти самый маленький элемент в отсортированном списке.
Задачи, для которых подойдёт шаблон K-Way слияние:
- слияние K-сортированных списков (средний);
- K-пары с самыми большими суммами (сложный).
14. Топологическая сортировка
Топологическая сортировка используется для нахождения линейного порядка элементов, которые зависят друг от друга. Например, если событие «Б» зависит от события «A», то «A» предшествует «Б» в топологическом порядке.
Этот шаблон — простой способ понять методику выполнения топологической сортировки набора элементов.
Шаблон работает так:
- Инициализация.
- Храните график в списках смежности, используя HashMap.
- Для нахождения всех источников используйте HashMap, чтобы сохранить количество степеней.
- Постройте график и найдите степени всех вершин.
- Постройте график из входных данных и заполните хэш-карту степенями.
- Найдите все источники.
- Все вершины с «0» степенями будут источниками и будут храниться в очереди.
- Сортировка.
- Для каждого источника сделайте следующее:
- добавьте его в отсортированный список,
- получите все дочерние элементы из графа,
- уменьшите степень каждого дочернего элемента на 1,
- если степень дочернего элемента становится «0», добавьте её в очередь источников.
- Повторяйте, пока исходная очередь не станет пустой.
- Для каждого источника сделайте следующее:


Как определить, когда следует использовать шаблон Топологической сортировки?
- задача связана с графами, которые не имеют направленных циклов;
- нужно обновить все объекты в отсортированном порядке;
- есть класс объектов, которые следуют определённому порядку.
Задачи, для которых подойдёт шаблон Топологической сортировки:
- планирование задач (средний);
- минимальная высота дерева (сложный).
[customscript]techrocks_custom_after_post_html[/customscript]
[customscript]techrocks_custom_script[/customscript]

